Research

Background info on Persistent Laplacians

Projects

Persistent Laplacian Library

I am working on a C++ library (with Python bindings) to efficiently compute many persistent Laplacian variations, unifying some disparate projects from multiple research groups in an efficient and user-friendly tool.

With preliminary testing, an experiment with the PDFL (below) that took 1.5 hours on 1 core of MSU’s High Performance Computing Cluster (HPCC) now takes about 12 seconds on 1 core of my laptop.

A Persistent Topological Laplacian for Directed Flag Complexes

Paper on arxiv, code on GitHub.

By combining persistent topological Laplacians with the directed flag complex (aka directed clique complex), we made the Persistent Directed Flag Laplacian (PDFL), which can glean information about the persistent homology and more. This builds on the fast persistent homology tool, Flagser, which was built similarly to Ripser: Computing Persistent Homology of Directed Flag Complexes by Daniel Lütgehetmann et al., 2020.

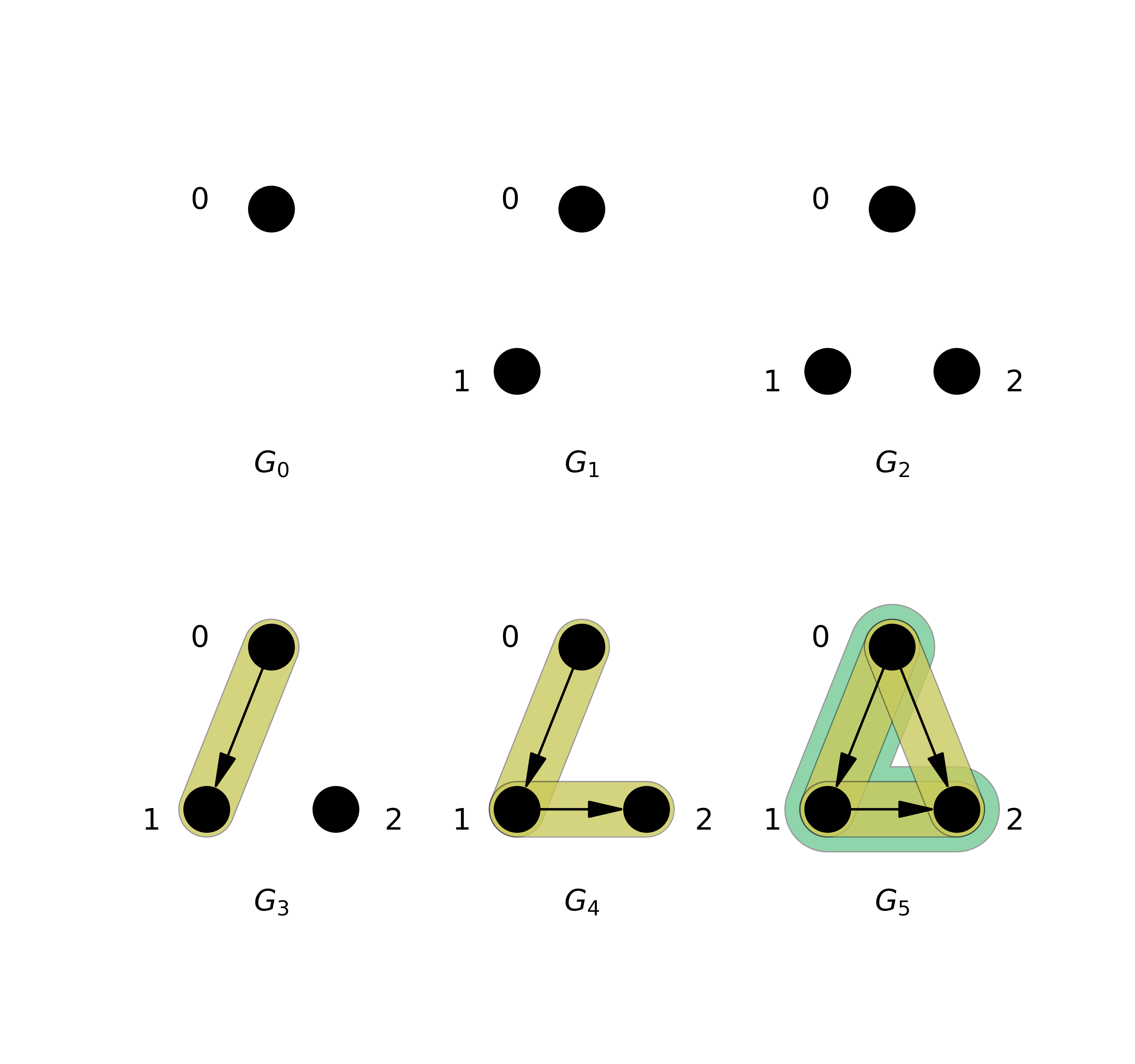
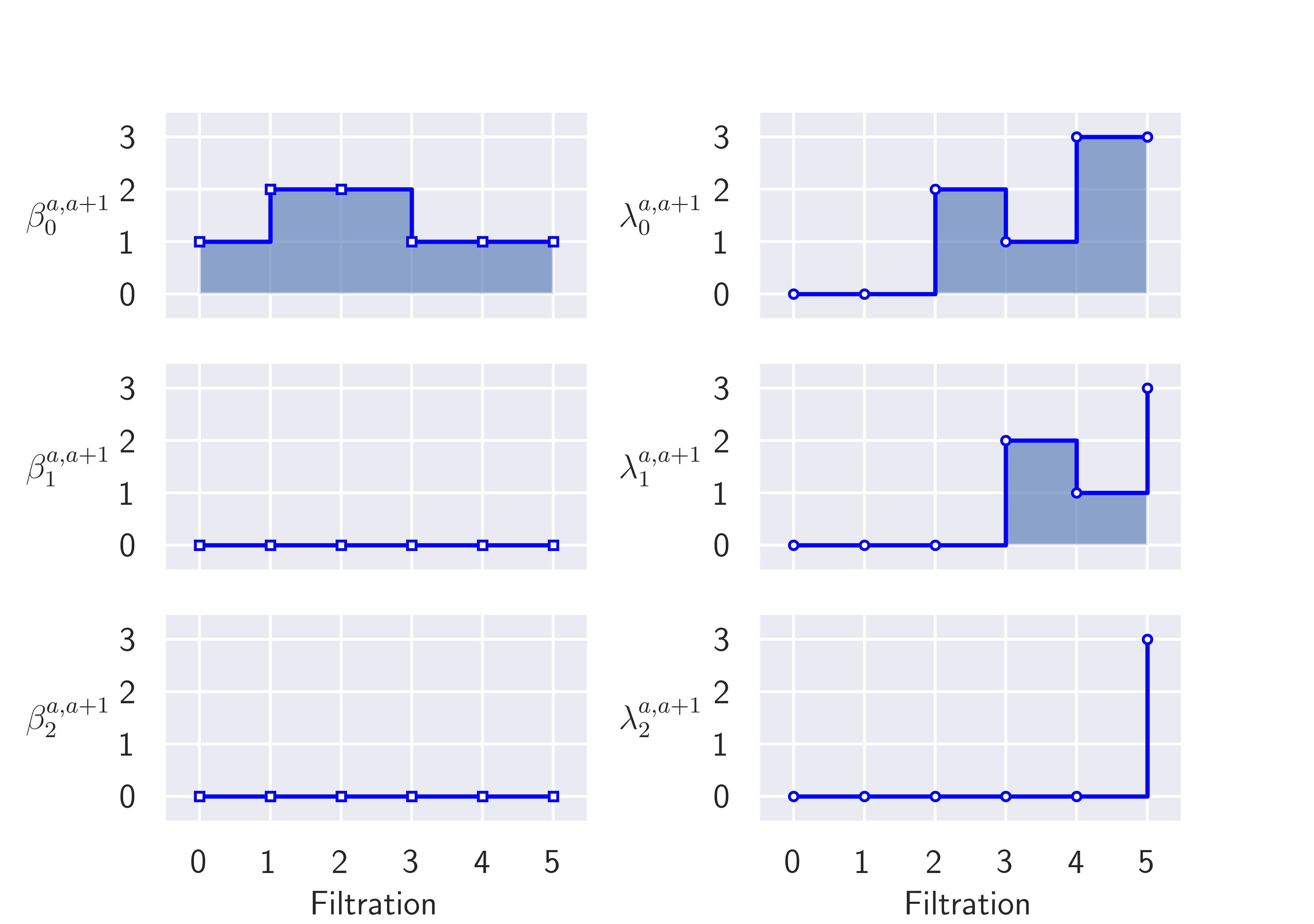
Here is a picture of a small filtered complex using a triangle, its persistent Betti numbers \(\beta\) and the least nonzero persistent Eigenvalues \(\lambda\).

Adaptive pseudo-time methods for solving the Nonlinear Poisson-Boltzmann Equation

This project is the basis for this paper, Ullah et al., 2023, and my master’s thesis. This work was completed with Shan Zhao’s research group at the University of Alabama.